Triangular Grid

COLOSSAL CITADELS uses triangular grid instead of common hex or square grids.

This is a development blog, and all published in-game materials are subject of change

I will give you some implementations of most used computations on triangular grid. I recommend to come up with this by yourself, but if you’re in hurry, you can just copy from this article or use my header-only library.

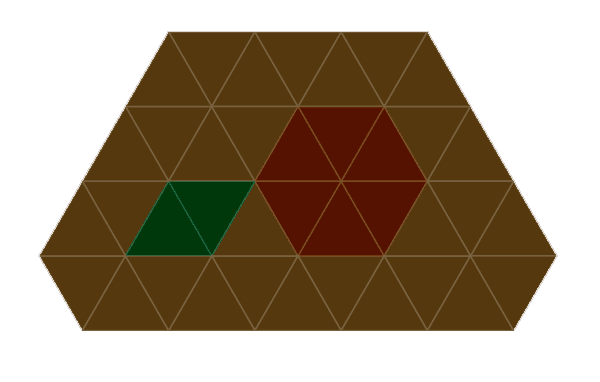
Why Is It Awesome?

• Triangular grid can include both square and hex grids. Actually, not squares, but rhombuses, but if you want, you can use half square triangles instead of equilateral ones
• Bastions use acute angles. It’s possible to build variety of bastion fort-like structures and utilize their potential in battles

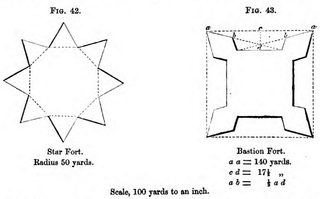
• Tight formations with alternating units can be represented as lines in triangular grid. These straight lines can have six directions and turn smoothly.
• Triangles can represent complex shapes. That is useful base for fortresses and streets, and interesting symmetrical shapes can be used for spells.

Coordinate Representation

Most convenient option is to represent is as square grid coordinate PLUS half-square side which can be either 0 or 1.

struct TilePosition {
    int x, y, s;
};

Conversions

Most common operations are various conversions.

Index <-> Coordinates

inline int toIndex(const Pos& pos, int gridWidth)
{
    return pos.x * 2 + pos.y * gridWidth * 2 + pos.s;
}

inline Pos fromIndex(int i, int gridWidth)
{
    return Pos{(i / 2) % gridWidth, (i / 2) / gridWidth, i % 2};
}

World <-> Coordinates

struct Vec2 {
    float x, y;
};

We will need constants for representing tile size in world space. Let’s just use these

namespace DefaultConstants
{
    const float Height = 150.f;
    const float Side = 173.20508075689f;
}

using Vec2 = std::pair<float, float>;

inline Vec2 gridToWorld(
    const Pos& pos,
    float worldspaceTriangleSide,
    float worldspaceTriangleHeight)
{
    return Vec2{
        pos.x * worldspaceTriangleSide + pos.y * worldspaceTriangleSide / 2.f,
        pos.y * worldspaceTriangleHeight
    };
}

inline Pos worldToGrid(const Vec2& pos)
{
    float y = std::get<1>(pos) / DefaultConstants::Height;
    float x = std::get<0>(pos) / DefaultConstants::Side - y / 2.f;
    bool s = (x - floor(x) + y - floor(y)) > 1.f;
    return Pos{int(x), int(y), int(s)};
}

Trianglular Grid <-> Square Grid

It’s just as simple as taking x and y components and adding or removing third coordinate from them.

Tile Distance

To calculate tile distance you can use Manhattan distance with addition of third component difference.

inline int distance(const Pos& a, const Pos& b)
{
    auto dx = a.x - b.x;
    auto dy = a.y - b.y;
    auto ds = a.s - b.s;
    return abs(dx) + abs(dy) + abs(dx + dy + ds);
}

Sources

All these functions plus some others (e.g. for calculating adjacent tiles) are included in my tiny header library. Feel free to use it, it’s published under CC0.